Описание алгоритма кластеризации из книги Advanced Algorithms and Data Structures Final Release 2021 by Marcello La Rocca

Page 419, Section 12.3.1 Напрямую VS Достижимый по плотности

Для понимания как DBSCAN работает, нам необходимо начать с нескольких определений. Используйте рис 12.0 в качестве справки при чтении, чтобы проверить ваше понимание:

• Точка p, на рис 12.9 називается центральной точкой потому что там есть по крайней мере min-Points точек (включая саму p) на расстоянии (епсилон) от нее \(\epsilon\) (где в примере minPoints==3)

• Точка q напрямую достижима из p потому что точка q входит в расстояние от ** \(\epsilon\) ** до p, которая является центральной точкой. Точка может только напрямую быть достижима из центральной точки.

• Точка w достижима (или равнозначно достижима по плотности density-reachable) из центральной точки (так как p) через путь основных точек p=w1, ..., wn=w, если каждая wi+1 напрямую достижима из wi. Из предыдущего определения прямой доступности, следует что все точки по пути, кроме w, должны быть центральными точками.

• Любые две точки которые достижимы между собой по плотности, будут определены в тот же самый кластер.

• Если есть какая либо точка r что не достижима из любых других точек что входят в набор данных, тогда r (и все точки такие как r) отмечаются как выброс (или шум).

Алгоритм построем на концепции центральных точек: каждая из них имеет по крайней мере определенное количество соседей на определенном расстоянии. Это можно увидеть также под другим углом: центральные точки это точки в областях с наименьшей плотностью. Центральные точки (такие как p, q, и так далее на рисунке 12.9) которые достижимы (то есть смежные) по отношению друг к другу принядлежат одному и тому же кластеру. Почему? Потому что мы предполагаем области с высокой плотностью (в отличии от большинства с низкой плотностью данных) определяют кластеры. Но все точки на расстоянии ** \(\epsilon\) ** от центральных точек p принадлежат тому же самому кластеру как p тоже.

Рисунок 12.9

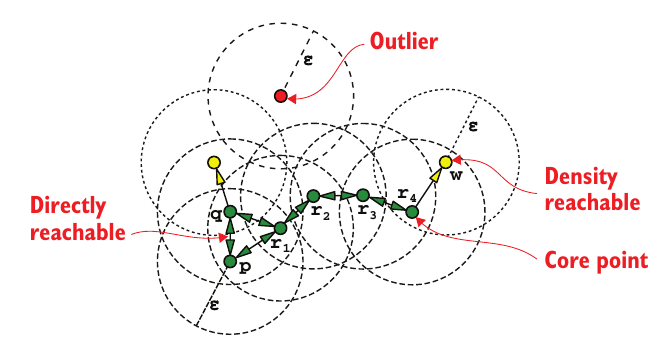
Центральные точки, напрямую достижимые точки и достижимые по плотности точки с учетом радиуса ** \(\epsilon\) ** и порогом minPoints (минимальное количество точек в центральном регионе) равным 3; следовательно, центральные точки должны иметь по крайне мере двух соседей с учетом расстояния ** \(\epsilon\) **.